Syllsbus
3B04CSC
Data Structure
No. of Contact Hours / Week: Theory: 3 & Lab 3 Credit: 4
Aim:
To familiarize the students with the methodology of computer science.
Objectives:
1. To introduce the concept of analysis of algorithms and ability to compare algorithms based on
time and space complexity.
2. To familiarize with selected linear and nonlinear data structures.
3. To enhance skill in programming.
4. To inculcate systematic approach to programming.
5. Develop ability to select appropriate data structure for a given problem.
Module I
Data structures: Definition and Classification. Analysis of Algorithms : Apriori Analysis; Asymptotic notation; Time complexity using O notation; Average, Best and Worst complexities. Arrays:- Operations; Number of elements; Array representation in memory. Polynomial- Representation with arrays; Polynomial addition. Recursive algorithms: examples – factorial and Tower of Hanoi problem.
Module II
Search : Linear and Binary search; Time complexity; comparison. Sort : Insertion, bubble, selection, quick and merge sort; Comparison of Sort algorithms.
Module III
Stack: Operations on stack; array representation. Application of stack- i. Postfix expression evaluation. ii. Conversion of infix to postfix expression. Queue : Operation on queue. Array Implementation; Limitations; Circular queue; Dequeue and priority queue. Application of queue: Job scheduling.
Module IV
Linked list – Comparison with arrays; representation of linked list in memory. Singly linked list- structure and implementation; Operations – traversing/printing; Add new node; Delete node; Reverse a list; Search and merge two singly linked lists. Stack with singly linked list. Circular linked list – advantage. Queue as Circular linked list. Doubly linked list – structure; Operations – Add/delete nodes; Print/traverse. Advantages.
Module V
Tree and Binary tree: Basic terminologies and properties; Linked representation of Binary tree; Complete and full binary trees; Binary tree representation with array. Tree traversal : Recursive inorder, preorder and postorder traversals. Binary search tree-Definition and operations (Create a BST, Search, Time complexity of search).
Text Book:
Data Structures and Algorithms: Concepts, Techniques and Applications; GAV Pai, Mc Graw Hill, 2008.
Reference Books:
1. Data Structures in C, Achuthsankar and Mahalekshmi, PHI, 2008
2. Fundamentals of Data structures in C++ , 2nd Edn, Horowitz Sahni, Anderson,Universities Press
3. Classic Data structures, Samanta, Second Edition, PHI
Model Question Paper
b A data structure is said to be ………..if its elements form a sequence.
c. A ………..is nothing but an array of characters.
d An array of pointers to strings stores ……..of the strings
e The ‘\O’ character indicates………………….
f. A matrix is called sparse when……..
g O notation stands for …..
h Basic operations in linked list are ………
2. What is Apriori Analysis
3. How to delete an element from the linked list
4. Define data structure
5. What is a sparse matrix?
6. What is garbage collection?
7. What is compaction?
8. What is the use of stack in real life?
9. Define dynamic data structure
10. What is multi stacks?
11. What is the complexity of algorithms?
12. Transform following prefix expression into infix a) +A-BC b)+-$ABC*D**EFG
13. Explain binary search in detail.
14. Explain advantageous of circular linked list.
15. Write program to which count number of words in a given text.
16. How to delete elements from a double link list
17. What is a sparse matrix explain
18. Write a program that would accept an expression in infix form and convert it to a
prefix form
19. What are the different operations on linked list? Explain
20. What are the advantages of binary tree search?
21. Compare different sorting algorithms
Short Answer Type Questions
1. What is an array?
2.What you mean by Data Structures?
3. How will you represent an array?
4. What are the different types of linear data structures?
5. What are the different types of non-linear data structures?
One Word type Questions
1. ________is a step by step procedure to solve a particular problem
2. ____________is a matrix with most of the elements are zeroes
3. _________is a quadratic time complexity
4.__________is the total space used to execute a program
5. A function that call itself is known as ___________
6. Time Complexity of linear search algorithm is _________
7. O(1) is called __________
8. FIFO means ____________
9. Queue follows __________manner
10. LIFO means ________
11. Stack follows ___________maner
One word question and answers
Model Question Paper
3B04CSC Data Structure
Time: 3 Hrs Max. Marks: 40
SECTION A
1. One word answer (8 x 0.5 = 4 marks)
a . A 2-D array is also called ……………………b A data structure is said to be ………..if its elements form a sequence.
c. A ………..is nothing but an array of characters.
d An array of pointers to strings stores ……..of the strings
e The ‘\O’ character indicates………………….
f. A matrix is called sparse when……..
g O notation stands for …..
h Basic operations in linked list are ………
SECTION B
Write short notes on ANY SEVEN of the following questions (7 x 2 = 14 marks)
3. How to delete an element from the linked list
4. Define data structure
5. What is a sparse matrix?
6. What is garbage collection?
7. What is compaction?
8. What is the use of stack in real life?
9. Define dynamic data structure
10. What is multi stacks?
11. What is the complexity of algorithms?
SECTION C
Answer ANY FOUR of the following questions (4 x 3 = 12 marks)
13. Explain binary search in detail.
14. Explain advantageous of circular linked list.
15. Write program to which count number of words in a given text.
16. How to delete elements from a double link list
17. What is a sparse matrix explain
SECTION D
Write an essay on ANY TWO of the following questions (2 x 5 = 10 marks)
prefix form
19. What are the different operations on linked list? Explain
20. What are the advantages of binary tree search?
21. Compare different sorting algorithms
Short Answer Type Questions
1. What is an array?
2.What you mean by Data Structures?
3. How will you represent an array?
4. What are the different types of linear data structures?
5. What are the different types of non-linear data structures?
One Word type Questions
1. ________is a step by step procedure to solve a particular problem
2. ____________is a matrix with most of the elements are zeroes
3. _________is a quadratic time complexity
4.__________is the total space used to execute a program
5. A function that call itself is known as ___________
6. Time Complexity of linear search algorithm is _________
7. O(1) is called __________
8. FIFO means ____________
9. Queue follows __________manner
10. LIFO means ________
11. Stack follows ___________maner
One word question and answers
Q 1 - Which one of the below is not divide and conquer approach?
Answer : B
Explanation
Among the options, only Merge sort divides the list in sub-list, sorts and then merges them together
Answer : C
Explanation
Stack uses push() to insert an item in stack, and pop() to remove the top item from stack.
Q 3 - The following formula will produce
Fn = Fn-1 + Fn-2
Answer : B
Explanation
Fibonacci Series generates subsequent number by adding two previous numbers.
Answer : C
Explanation
Every connected graph at least has one spanning tree.
Q 5 - Time complexity of Depth First Traversal of is
Answer : A
Explanation
Using Depth First Search, we traverse the whole graph i.e. visiting all Vertices and Edges.
Q 6 - Match the following −
| (1) Bubble Sort | (A) Ο(n) |
| (2) Shell Sort | (B) Ο(n2) |
| (3) Selection Sort | (C) Ο(n log n) |
Answer : B
Explanation
Q 7 - Index of arrays in C programming langauge starts from
Answer : A
Explanation
Arrays, in C, starts from 0 which is mapped to its base address.
Q 8 - Recursion uses more memory space than iteration because
Answer : B
Explanation
Recursion uses stack but the main reason is, every recursive call needs to be stored separately in the memory.
Q 9 - If we choose Prim's Algorithm for uniquely weighted spanning tree instead of Kruskal's Algorithm, then
Answer : B
Explanation
Regardless of which algorithm is used, in a graph with unique weight, resulting spanning tree will be same.
Q 10 - Which of the following algorithm does not divide the list −
Answer : A
Explanation
Linear search, seaches the desired element in the target list in a sequential manner, without breaking it in any way.
1. Preorder is
- depth first order
- breadth first order
- topological order
- linear order
Answer And Explanation
Answer: Option A
3. ++i is equivalent to
- i = i + 2
- i = i + 1
- i = i + i
- i = i - 1
Answer And Explanation
Answer: Option B
5. Deletion from one end and insertion from other end is
- stack
- branch
- tree
- queue
Answer And Explanation
Answer: Option D
Answer: Option D
6. Which statement we should ignore in structure programming
- WHILE-DO
- GO-TO
- IT-ELSE
- SWITCH
Answer And Explanation
Answer: Option B
Answer: Option B
Queue follows methodology of
- LIFO
- FILO
- FIFO
- MFU
Delete operation in a queue can be performed using function
- popqueue()
- deletequeue()
- removequeue()
- dequeue()
Binary search algorithm have a run-time complexity of
- O(1)
- O(n)
- O(log 1)
- O(log n)
Insert operation in a queue can be performed using function
- enqueue()
- inqueue()
- pushqueue()
- insertqueue()
A search that is made over all items one by one is called
- Binary search
- Interpolation search
- Linear search
- Bubble search
If desired data is not found in binary search, then rest of list is
- Divided into 2 parts
- Divided into 3 parts
- Divided into 4 parts
- Divided into no parts
Worst-case complexity of bubble-sort is
- O(log n)
- ?(n)
- O(n^2)
- ?(n^2)
In hash table, data is stored in format of
- Array
- Linked list
- Pointers
- Queues
A data structure that stores data in an associative manner is known to be
- Queue
- Stacks
- Hash table
- Linked List
If sorting operation uses equal or more space than required, is called
- Not-in place sorting
- Not-on place sorting
- Not-on element sorting
- Not-in value sorting
Bubble sort is an example of form
- In place sorting
- In value sorting
- Not-in place sorting
- Not-on place sorting
Algorithms that does not require any extra space
- In value sorting
- In place sorting
- On place sorting
- On value sorting
Sorting operation requires temporary storage for few
- Data entries
- Data entities
- Data elements
- Data nodes
Sorting operation requires some extra space for
- Comparison
- Buffering
- Queuing
- Linking
Linked list is of basic
- 2 types
- 3 types
- 4 types
- 5 types
A sequence of data structures connected together through links are known to be
- Connected list
- Linked list
- Traversed link
- Compound List
A linked list type that navigates for an item in forward manner only, is called
- Simple Linked List
- Linear Linked List
- Doubly Linked List
- Circular linked List
Second most used data structure after array is
- Queue
- Stack
- Hash table
- Linked List
A linked list type that navigates for an item in forward and backward direction is called
- Doubly Linked List
- Circular linked List
- Linear Linked List
- Absolute linked List
4. Repeated execution of simple computation may cause compounding of
- round off errors
- syntax errors
- run time errors
- logic errors
Answer And Explanation
Answer: Option A
SHORT ANSWER TYPE QUESTIONS
Apriori analysis of algorithms :
it means we do analysis (space and time) of an algorithm prior to running it on specific system - that is, we determine time and space complexity of algorithm by just seeing the algorithm rather than running it on particular system (with different processor and compiler).
Aposteriory analysis of algorithms :
it means we do analysis of algorithm only after running it on system. It directly depends on system and changes from system to system.
Applications of stack
1. Infix to postfix conversion
2.postfix expression evaluation
Garbage Collection (GC)
Garbage collection (GC) is a dynamic approach to automatic memory management and heap allocation that processes and identifies dead memory blocks and reallocates storage for reuse. The primary purpose of garbage collection is to reduce memory leaks.
GC implementation requires three primary approaches, as follows:
- Mark-and-sweep - In process when memory runs out, the GC locates all accessible memory and then reclaims available memory.
- Reference counting - Allocated objects contain a reference count of the referencing number. When the memory count is zero, the object is garbage and is then destroyed. The freed memory returns to the memory heap.
- Copy collection - There are two memory partitions. If the first partition is full, the GC locates all accessible data structures and copies them to the second partition, compacting memory after GC process and allowing continuous free memory.
Garbage collection (GC) is a dynamic approach to automatic memory management and heap allocation that processes and identifies dead memory blocks and reallocates storage for reuse. The primary purpose of garbage collection is to reduce memory leaks.
GC implementation requires three primary approaches, as follows:
- Mark-and-sweep - In process when memory runs out, the GC locates all accessible memory and then reclaims available memory.
- Reference counting - Allocated objects contain a reference count of the referencing number. When the memory count is zero, the object is garbage and is then destroyed. The freed memory returns to the memory heap.
- Copy collection - There are two memory partitions. If the first partition is full, the GC locates all accessible data structures and copies them to the second partition, compacting memory after GC process and allowing continuous free memory.
Data compaction
Removal of redundant information from a file or data stream. The term data compression is commonly used to mean the same thing, although, strictly, while compression permits the loss of information in the quest for brevity, compaction is lossless. The effects of compaction are thus exactly reversible.
Advantages and Dis-advantages of array?
Tree Traversal
Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −
- In-order Traversal
- Pre-order Traversal
- Post-order Traversal
Algorithm : Inorder
Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.
Algorithm : Pre-order
Until all nodes are traversed −
Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.
Algorithm : Post-order
Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.
In-place Sorting and Not-in-place Sorting
Sorting algorithms may require some extra space for comparison and temporary storage of few data elements. These algorithms do not require any extra space and sorting is said to happen in-place, or for example, within the array itself. This is called in-place sorting.
Bubble sort is an example of in-place sorting.
However, in some sorting algorithms, the program requires space which is more than or equal to the elements being sorted. Sorting which uses equal or more space is called not-in-place sorting.
Merge-sort is an example of not-in-place sorting.
Applications of binary trees
- Binary Search Tree - Used in many search applications where data is constantly entering/leaving, such as the
mapandsetobjects in many languages' libraries. - Binary Space Partition - Used in almost every 3D video game to determine what objects need to be rendered.
- Binary Tries - Used in almost every high-bandwidth router for storing router-tables.
- Hash Trees - used in p2p programs and specialized image-signatures in which a hash needs to be verified, but the whole file is not available.
- Heaps - Used in implementing efficient priority-queues, which in turn are used for scheduling processes in many operating systems, Quality-of-Service in routers, and A* (path-finding algorithm used in AI applications, including robotics and video games). Also used in heap-sort.
- Huffman Coding Tree (Chip Uni) - used in compression algorithms, such as those used by the .jpeg and .mp3 file-formats.
- GGM Trees - Used in cryptographic applications to generate a tree of pseudo-random numbers.
- Syntax Tree - Constructed by compilers and (implicitly) calculators to parse expressions.
- Treap - Randomized data structure used in wireless networking and memory allocation.
- T-tree - Though most databases use some form of B-tree to store data on the drive, databases which keep all (most) their data in memory often use T-trees to do so.
Data Definition
Data Definition defines a particular data with the following characteristics.
- Atomic − Definition should define a single concept.
- Traceable − Definition should be able to be mapped to some data element.
- Accurate − Definition should be unambiguous.
- Clear and Concise − Definition should be understandable.
Data Object
Data Object represents an object having a data.
Data Type
Data type is a way to classify various types of data such as integer, string, etc. which determines the values that can be used with the corresponding type of data, the type of operations that can be performed on the corresponding type of data. There are two data types −
- Built-in Data Type
- Derived Data Type
Built-in Data Type
Those data types for which a language has built-in support are known as Built-in Data types. For example, most of the languages provide the following built-in data types.
- Integers
- Boolean (true, false)
- Floating (Decimal numbers)
- Character and Strings
Derived Data Type
Those data types which are implementation independent as they can be implemented in one or the other way are known as derived data types. These data types are normally built by the combination of primary or built-in data types and associated operations on them. For example −
- List
- Array
- Stack
- Queue
Basic Operations
The data in the data structures are processed by certain operations. The particular data structure chosen largely depends on the frequency of the operation that needs to be performed on the data structure.
- Traversing
- Searching
- Insertion
- Deletion
- Sorting
- Merging
Important Terms Related To Tree
Following are the important terms with respect to tree.
- Path − Path refers to the sequence of nodes along the edges of a tree.
- Root − The node at the top of the tree is called root. There is only one root per tree and one path from the root node to any node.
- Parent − Any node except the root node has one edge upward to a node called parent.
- Child − The node below a given node connected by its edge downward is called its child node.
- Leaf − The node which does not have any child node is called the leaf node.
- Subtree − Subtree represents the descendants of a node.
- Visiting − Visiting refers to checking the value of a node when control is on the node.
- Traversing − Traversing means passing through nodes in a specific order.
- Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on.
- keys − Key represents a value of a node based on which a search operation is to be carried out for a node.
Common Asymptotic Notations
Following is a list of some common asymptotic notations −
| constant | − | Ο(1) |
| logarithmic | − | Ο(log n) |
| linear | − | Ο(n) |
| n log n | − | Ο(n log n) |
| quadratic | − | Ο(n2) |
| cubic | − | Ο(n3) |
| polynomial | − | nΟ(1) |
| exponential | − | 2Ο(n) |
Divide and Conquer
In divide and conquer approach, the problem in hand, is divided into smaller sub-problems and then each problem is solved independently. When we keep on dividing the subproblems into even smaller sub-problems, we may eventually reach a stage where no more division is possible. Those "atomic" smallest possible sub-problem (fractions) are solved. The solution of all sub-problems is finally merged in order to obtain the solution of an original problem.
The following computer algorithms are based on divide-and-conquerprogramming approach −
- Merge Sort
- Quick Sort
- Binary Search
- Strassen's Matrix Multiplication
- Closest pair (points)
Dynamic Programming
Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems. But unlike, divide and conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are remembered and used for similar or overlapping sub-problems.
The following computer problems can be solved using dynamic programming approach −
- Fibonacci number series
- Knapsack problem
- Tower of Hanoi
- All pair shortest path by Floyd-Warshall
- Shortest path by Dijkstra
- Project scheduling
Types of Linked List
Following are the various types of linked list.
- Simple Linked List − Item navigation is forward only.
- Doubly Linked List − Items can be navigated forward and backward.
- Circular Linked List − Last item contains link of the first element as next and the first element has a link to the last element as previous.
Basic Operations Linked List
Following are the basic operations supported by a list.
- Insertion − Adds an element at the beginning of the list.
- Deletion − Deletes an element at the beginning of the list.
- Display − Displays the complete list.
- Search − Searches an element using the given key.
- Delete − Deletes an element using the given key.
Advantages of linked lists:
1. Linked lists are dynamic data structures. i.e., they can grow or shrink during the execution of a program.
2. Linked lists have efficient memory utilization. Memory is allocated whenever it is required and it is de-allocated (removed) when it is no longer needed.
3. Insertion and Deletions are easier and efficient. Linked lists provide flexibility in inserting a data item at a specified position and deletion of the data item from the given position.
4. Many complex applications can be easily carried out with linked lists.
Disadvantages of linked lists:
1. It consumes more space because every node requires a additional pointer to store address of the next node.
2. Searching a particular element in list is difficult and also time consuming.
3. Reverse Traversing is difficult in linked list
Types of Linked Lists:
Basically we can put linked lists into the following...
1. Single Linked List.
2. Circular Single Linked List.
3. Double Linked List.
4. Circular Double Linked List.
5. Header Linked list
6. Multi Linked List.
Applications of linked list:
1. Linked lists are used to represent and manipulate polynomial.
2. Hash tables use linked lists for collission resolution.
3. Any "File Requester" dialog uses a linked list.
4. Linked lists use to implement stack, queue, trees and graphs.
5. To implement the symbol table in compiler construction.
Some common variables use in linked list
START : Store the address of first node.
AVAIL : Store the address of first free space.
PTR : Points to node that is currently being accessed.
NUll : End of list.
NEW_NODE :To store address of newly created node.
Polynomial
A polynomial p(x) is the expression in variable x which is in the form (axn + bxn-1 + …. + jx+ k), where a, b, c …., k fall in the category of real numbers and 'n' is non negative integer, which is called the degree of polynomial.
An essential characteristic of the polynomial is that each term in the polynomial expression consists of two parts:
Example:
10x2 + 26x, here 10 and 26 are coefficients and 2, 1 is its exponential value.
Points to keep in Mind while working with Polynomials:
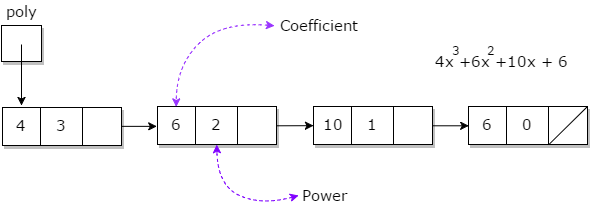

Representation of Polynomial
Polynomial can be represented in the various ways. These are:
Write a program to perform queue operation
- #include<iostream.h>
- #include<conio.h>
- #include<stdlib.h>
- #define SIZE 5
- int q[SIZE],front=0,rear=0;
- void main()
- {
- int ch;
- clrscr();
- void enqueue();
- void dequeue();
- void display();
- while(1)
- {
- cout<<"\n 1. add element";
- cout<<"\n 2. remove element";
- cout<<"\n 3.display";
- cout<<"\n 4.exit";
- cout<<"\n enter your choice:";
- cin>>ch;
- clrscr();
- switch(ch)
- {
- case 1:
- enqueue();
- break;
- case 2:
- dequeue();
- break;
- case 3:
- display();
- break;
- case 4:
- exit(0);
- default:
- cout<<"\n invalid choice";
- }
- }
- }
- void enqueue()
- {
- int no;
- if (rear==SIZE && front==0)
- cout<<"queue is full";
- else
- {
- cout<<"enter the num:";
- cin>>no;
- q[rear]=no;
- }
- rear++;
- }
- void dequeue()
- {
- int no,i;
- if (front==rear)
- cout<<"queue is empty";
- else
- {
- no=q[front];
- front++;
- cout<<"\n"<<no<<" -removed from the queue\n";
- }
- }
- void display()
- {
- int i,temp=front;
- if (front==rear)
- cout<<"the queue is empty";
- else
- {
- cout<<"\n element in the queue:";
- for(i=temp;i<rear;i++)
- {
- cout<<q[i]<<" ";
- }
- }
- }




















U can add some notes also
ReplyDeleteOfcource
ReplyDelete